工作探索

SURVEY & STUDY
法律中的数学思维(二)——数模思维
陈宣延
公平算术
数学建模也是“计算”公平的有力工具。我们知道,公平是法律的价值之一。当人们提及法律时,头脑中就会浮现“公平正义”的概念。数学是计算公平的有效尺度。在全国和地方各级人民代表大会中,如何公平分配席位涉及公民权利保障的根本性问题。目前人大席位的分配一般方法是:
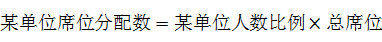 。 。
先讨论由两个单位公平分分配席位的情况,具体如表所示:
|
单位
|
人数
|
席位数
|
每席位代表人数
|
|
单位A
|
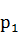
|
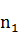
|
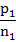
|
|
单位B
|
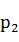
|
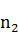
|
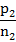
|
图1 AB两个单位公平分分配席位的情况
要满足公平,应该有
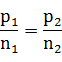
但这一般不成立。注意到等式不成立时,有:若
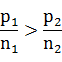
则说明对单位A不公平;若
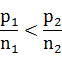
则说明对单位B不公平。
因此,可以考虑用公式
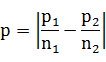
来衡量分配不公平程度,不过此公式有不足之处(绝对数的特点),如果两个单位的人数和席位为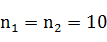 , ,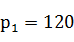 , ,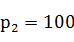 ,算得 ,算得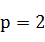 ;另两个单位的人数和席位为 ;另两个单位的人数和席位为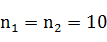 , ,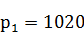 , ,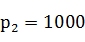 ,算得 ,算得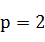 。虽然在两种情况下都有 。虽然在两种情况下都有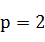 ,但显然第二种情况比第一种公平。 ,但显然第二种情况比第一种公平。
下面采用相对标准对公式给予改进。定义席位分配的相对不公平标准公式如下:
若
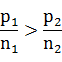
定义
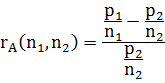
为对单位A的相对不公平值;
若
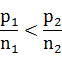
定义
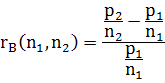
为对单位B的相对不公平值;由定义可知,对某单位的公平值越小,该单位在席位分配中越有利。因此可以用使不公平值越小的分配方案来减少分配中的不公平。
下面讨论通过使用不公平值的大小来确定分配方案。
设单位A的人数为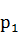 ,已有席位数为 ,已有席位数为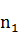 ;单位B的人数为 ;单位B的人数为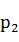 ,已经有席位数为 ,已经有席位数为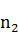 。再增加一个席位,分配给单位A和B时,有如下不公平值 。再增加一个席位,分配给单位A和B时,有如下不公平值
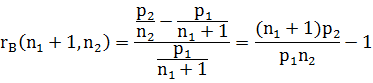
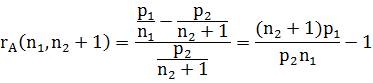
用不公平值公式来决定席位的分配。对于新的席位分配,若有
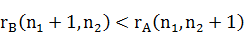
则增加的席位应给A,此时对不等式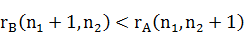 化简得 化简得
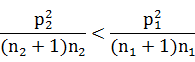
引入公式
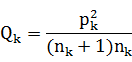
于是知道增加的席位分配可以由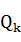 的最大值决定,它可以推广到多个组的一般情况。 的最大值决定,它可以推广到多个组的一般情况。
定义:用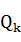 的最大值决定席位分配的方法称为“Q值法”。 的最大值决定席位分配的方法称为“Q值法”。
对多个组(m个组)的席位分配的Q值法可以描述为:
(1)先计算每个组的Q值,即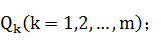
(2)求出其中最大值的Q值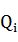 (若有多个最大值任选其中一个即可); (若有多个最大值任选其中一个即可);
(3)将席位分配给最大值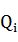 对应的第i组。 对应的第i组。
这种分配方法易于编程处理。下面举例说明该模型的运用。
例 某区三个单位甲、乙、丙设20个人大代表,丙最初单位人数和单位人大代表席位如下表所示:
|
单位
|
甲
|
乙
|
丙
|
总数
|
|
单位人数
|
100
|
60
|
40
|
200
|
|
单位人数比例
|
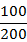
|
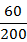
|
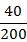
|
|
|
席位分配
|
10
|
6
|
4
|
20
|
图2 甲乙丙三个单位最初单位人数和单位人大代表席位
后来由于出现单位成员转单位的情况,各单位人数和人大代表席位有变动,如表:
|
单位
|
甲
|
乙
|
丙
|
总数
|
|
单位人数
|
100
|
60
|
40
|
200
|
|
单位人数比例
|
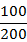
|
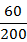
|
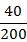
|
|
|
按比例
分配席位
<, /td>
|
10.3
|
6.3
|
3.4
|
20
|
|
席位分配
|
10
|
6
|
4
|
20
|
图3 甲乙丙三个单位现在单位人数和单位人大代表席位
由于总代表席位为偶数,使得在人大代表解决问题的表决中有时出现平局而不能达成一致意见,决定在增加一个人大代表,总席位数变为21个。
先按应分配的整数部分分配,余下的用Q值法分配。本问题的整数部分共分配了19席,如如下矩阵所示:
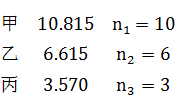
对第20席,根据Q值法,应将增加的席位给Q值最大的单位。通过Microsoft Visual
Basic 6.0,编写程序代码如下:
Option
Explicit
Option
Base 1
Private
Sub Form_Click()
Dim p%, n%, i%, shift$
Static Q(3)
For i = 1 To 3 Step 1
p = InputBox("please input the number of
people")
n = InputBox("please input the number of position")
Q(i) = p * p / ((n + 1) * n)
Next i
shift = Chr$(13) + Chr$(10)
Print "Q of the first group is"; CCur(Q(1)); shift; "Q of the
second group is"; CCur(Q(2)); shift; "Q of the third group is";
CCur(Q(3))
End
Sub
显示如下:
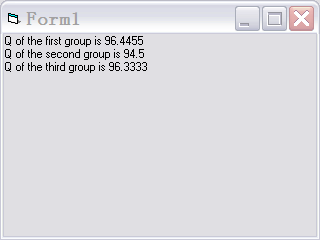
图4 对第20席Q值执行情况
可知第一组,也就是甲单位的Q值最大,故分配给甲单位。
对第21席的分配,根据Q值法,程序执行如下:
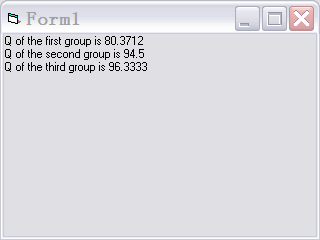
图5 对第21席Q值执行情况
可知第三组,也就是丙单位的Q值最大,故分配给丙单位。
综上所述,最后席位分配为:甲11席,乙6席,丙4席。同时说明该算法可以代码化,为自动化、数据化公平地计算席位有实际意义。
汉德模型
首先,我们设计两个函数,函数f(x)=B,函数g(x)=LP,其中B为“注意成本”,L为“损失额度”、P为“损失发生概率”。经验告诉我们,越注意避免风险,越要付出更多的注意成本,所以函数f(x)=B,“注意的程度”和“注意成本”呈正相关,该函数指“致害者预防未来事故的成本”;同理,经验告诉我们,随着注意程度提高,风险带来的损失越小,所以函数g(x)=LP,“注意的程度”和“损失额”呈负相关,该函数指“预期事故的可能性乘预期事故损失”。
其次,我们建立坐标系,横轴表示“注意的程度”;将具有相同属性的“注意成本”和“损失额”统一为“数额”用“$”表示纵轴。

图6
再次,由于函数f(x)=B呈正相关,得曲线B;同理,由于函数g(x)=LP,得曲线LP。
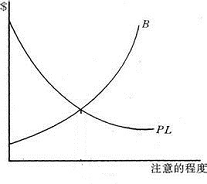
图7
再次,由图可知两曲线交于一点C*,从C*分为两个区域,左边的“I区”和右边得“II区”。
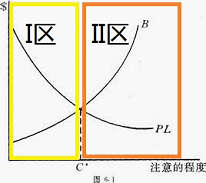
图8
再次,由图可知,在I区时,PL>B;在C*上时,PL=B;在II区时,PL<B。通过前面,我们知道,当PL>B时说明设置一项预防设施的成本小于预期风险造成的损失,说明此种情形是经济的;当PL<B时说明设置一项预防设施的成本大于预期风险造成的损失,说明此种情形是不经济的;通过上图我们可知当PL=B时,设置一项预防设施的成本等于预期风险造成的损失。
最后,就对“宁波老虎咬人事件”的分析看:死者亲属发声,称动物园管理有漏洞,称“不能给人翻进去的机会”,不过当PL<B时,动物园的注意成本过高(如每天派人在虎园时刻不停地巡逻等)对于动物园这一行业来说就是不经济,不利于动物园行业的发展;所以对于动物园而言,采用高墙和警示标语就做到了经济性,即PL>B,此时如果在PL>B下,动物园仍没有采取合理的预防措施(如高墙和警示标语等合理措施),则推定动物园有过错,应承担侵权责任。概言之,只有当动物园预防未来事故的成本小于预期事故的可能性乘预期事故损失时应该承担侵权责任。
需要指出的一点是,肯定有人会说,这里是一条人命的损失,人命能用金钱衡量吗?我们首先对遇难者表示哀悼,不过我们认为,不宜将道德情感过多纳入科学分析中来,生命无价是人们美好向往,这里暂且不讨论,然而在法律上,侵犯身体权、健康权和生命权的都由相应的赔偿金、赔偿金、死亡赔偿金等,生命在道德中的无价,不得不在法律中体现价格。所以“生命无价”告诉我们“勿伤他人”;“生命有价”是让我们给他人造成损害要赔偿,从而杜绝“同态复仇”,恢复社会秩序。因此这是两个层面的问题。我们知道,如果认为生命无价,我们的注意成本非常高,将B推向无穷,即B=∞,这样我们人为地将自己置身于风险的世界,我们害怕一切风险,因此我们的社会也不会发展,这显然是不合理的。
值得一提得是,这一模型是美国联邦上诉法院第二巡回庭著名法官勒·汉德在1947年美利坚合众国诉卡洛尔拖船公司(以下简称卡洛尔案)一案中正式提出,其中得“PL<B”即为著名得“汉德公式”。
结尾的话
笔者坚持:比知识本身更重要的是思维。从自然语言到数学语言再到程序语言,每一次语言的转变就是一次思维的变革,同一个事物从不同角度观察往往能更好的揭示事物的本质。所以,笔者认为:习法者须重视语言的训练,无论是自然语言、程序语言还是沟通自然语言和程序语言的数学语言。“训”来“训”去,智慧其中矣。
|

