工作探索

SURVEY & STUDY
法律中的数学思维(三)——条件概率思维
陈宣延
有时守旧势力之大以致于人们自己都很难意识到。明明深知“抱守残缺”的危害;却由于事物的纷繁复杂而常常被冲昏头脑。“颠倒的条件概率”是常常发生的概率学上的错误,对生活中一些鸡毛蒜皮之事估计有误,无伤大雅;但要是在法庭论证中把概率计算错了,对于被告人可能就是死生之大事。幸运地是,问题具有集聚性,只要对某一问题发生的时间、地点及其其他条件加以控制,就能很好的避免这类错误。
例 一个取自犯罪现场的DNA样品和另一个取自犯罪嫌疑人的DNA样品之间的“匹配概率”:公诉人的谬误指的是两种不同概率之间的混淆。‘匹配概率’所回答的是‘给定一个人无罪的前提下,个体DNA抽样鉴定和犯罪现场DNA样品相匹配的概率是多少?’但是法庭所应当考虑的问题是‘给定DNA’相互匹配,犯罪嫌疑人无罪的概率是多少?’这两个问题各自可能获得毫不相关的回答。
本例可用条件概率求解,设条件概率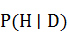 ,意思是说,在D的条件下,H的概率是多少?它可以用简单概率定义,只要 ,意思是说,在D的条件下,H的概率是多少?它可以用简单概率定义,只要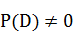 就有 就有
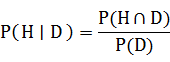
它的几何表示如下:
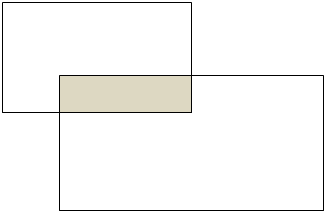
图1 条件概率的几何表示
回到上述案例,假定,有一从犯罪现场收集到的血迹样本,还有一取自犯罪嫌疑人的血样,接受DNA鉴定,所有的遗传特征指标都匹配。公诉人认为既然DNA匹配,那么假设该人无罪的概率仅为百万分之一。那么法官能不能把它视为有罪的强有力的证据否?
首先,我们要从刑事诉讼法中的“无罪推定原则”出发。一方面,在作为证据法基本原则的无罪推定下,其基本要求是,在被依法证明有罪之前,任何人都应被推定为无罪的人。在这里主要指公诉机关所提供的证据是考虑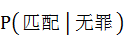 ,即给定一个人无罪的前提下,个体DNA抽样鉴定和犯罪现场DNA样品相匹配的概率是多少?另一方面,在作为刑事诉讼基本原则的无罪推定下,其基本含义是,未经法院做出生效的有罪判决,任何人都应被推定为法律上无罪的人。在这里主要是指法官面前所要考虑的问题是给定DNA匹配,被告人无罪的概率 ,即给定一个人无罪的前提下,个体DNA抽样鉴定和犯罪现场DNA样品相匹配的概率是多少?另一方面,在作为刑事诉讼基本原则的无罪推定下,其基本含义是,未经法院做出生效的有罪判决,任何人都应被推定为法律上无罪的人。在这里主要是指法官面前所要考虑的问题是给定DNA匹配,被告人无罪的概率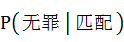 ,即给定DNA’相互匹配,犯罪嫌疑人无罪的概率是多少? ,即给定DNA’相互匹配,犯罪嫌疑人无罪的概率是多少?
其次,根据条件概率的定义,我们可得:
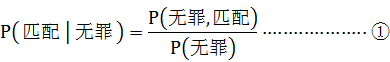
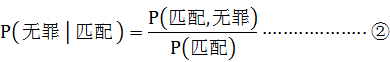
由此我们可以观察得知,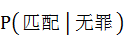 和 和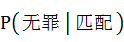 两个截然不同的概率,在①中,若 两个截然不同的概率,在①中,若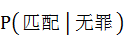 大,保持 大,保持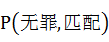 一定, 一定,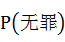 须小,反之亦然,即 须小,反之亦然,即
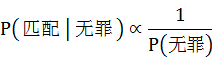
;
同理,在②中,若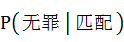 大,保持 大,保持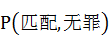 一定, 一定,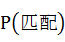 须小,反之亦然,即 须小,反之亦然,即
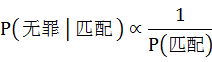
。
再次,若公诉机关在给定一个人无罪的前提下,个体DNA抽样鉴定和犯罪现场DNA样品相匹配的概率很高时,即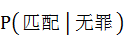 很高,若保持 很高,若保持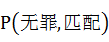 一定,则该人无罪的概率就很低,即 一定,则该人无罪的概率就很低,即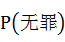 很低;如果法庭依据 很低;如果法庭依据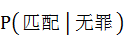 很高就推出 很高就推出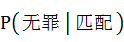 很低是不妥的,即认为公诉机关证据表明的匹配概率越高则法庭认定该人的无罪概率越低是不妥的,因为,其中的一种情况是,当 很低是不妥的,即认为公诉机关证据表明的匹配概率越高则法庭认定该人的无罪概率越低是不妥的,因为,其中的一种情况是,当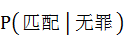 很高时, 很高时,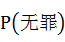 很低,而并不意味着 很低,而并不意味着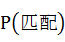 跟着很高,从而导致 跟着很高,从而导致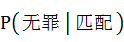 很低,也就是说 很低,也就是说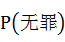 和 和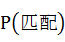 不一定是相背运动的,即高度匹配不能认为有罪,这里就是“颠倒的条件概率”谬误之渊薮。 不一定是相背运动的,即高度匹配不能认为有罪,这里就是“颠倒的条件概率”谬误之渊薮。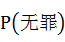 和 和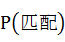 的认定还要考虑它们的样本空间和随机事件中的样本点,如果假设遗传特征只有两个来源:DNA和人群结构,那么 的认定还要考虑它们的样本空间和随机事件中的样本点,如果假设遗传特征只有两个来源:DNA和人群结构,那么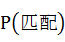 的样本空间至少包括这两种。 的样本空间至少包括这两种。
最后,我们知道,如果法庭由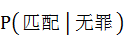 高错误地推出 高错误地推出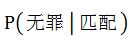 低,就排除了 低,就排除了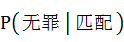 高的可能,就会出现“冤案”;同理,如果如果法庭由 高的可能,就会出现“冤案”;同理,如果如果法庭由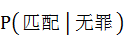 低错误地推出 低错误地推出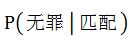 高,就排除了 高,就排除了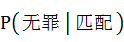 低的可能,就会出现“纵囚”。都是不公正的判决。我们知道因为根据积事件的概率性质可知 低的可能,就会出现“纵囚”。都是不公正的判决。我们知道因为根据积事件的概率性质可知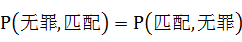 ,所以当 ,所以当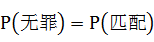 时或称为一种均衡,法庭才可能由 时或称为一种均衡,法庭才可能由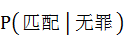 准确地推出 准确地推出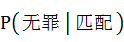 ,以为此时 ,以为此时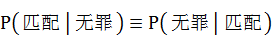 ,法庭这里犯的错误就是把这个等价式扩大适用了,从这个例子所获得最突出的教训就是: ,法庭这里犯的错误就是把这个等价式扩大适用了,从这个例子所获得最突出的教训就是: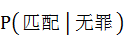 和 和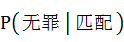 是两种不同的数量值,切不可加以混淆。 是两种不同的数量值,切不可加以混淆。
很可悲的是,一个无罪的人有可能进了监狱,而一个有罪的人却可能获得释放,只是因为法官错误地理解了条件概率,从而错误地理解了证据。 当然,建议每一个将做法官的人,都进修条件概率课程并通过考试,显然是不实际的,但是作为法官指导他们按某些原则行事,则完全是切实可行的。一个简洁的评述或讲解能避免条件概率和其翻转值加以混淆,从而减少法官出于无知作出荒谬的论证和主张。
|

